Authors:
(1) Maggie D. Bailey, Colorado School of Mines and National Renewable Energy Lab;
(2) Douglas Nychka, Colorado School of Mines;
(3) Manajit Sengupta, National Renewable Energy Lab;
(4) Aron Habte, National Renewable Energy Lab;
(5) Yu Xie, National Renewable Energy Lab;
(6) Soutir Bandyopadhyay, Colorado School of Mines.
Table of Links
Bayesian Hierarchical Model (BHM)
Appendix B: Regridding Coefficient Estimates
Abstract
Initial steps in statistical downscaling involve being able to compare observed data from regional climate models (RCMs). This prediction requires (1) regridding RCM output from their native grids and at differing spatial resolutions to a common grid in order to be comparable to observed data and (2) bias correcting RCM data, via quantile mapping, for example, for future modeling and analysis. The uncertainty associated with (1) is not always considered for downstream operations in (2). This work examines this uncertainty, which is not often made available to the user of a regridded data product. This analysis is applied to RCM solar radiation data from the NA-CORDEX data archive and observed data from the National Solar Radiation Database housed at the National Renewable Energy Lab. A case study of the mentioned methods over California is presented.
1 Introduction
Earth system models and regional climate models (RCM) are standard tools used to quantify and understand future changes in climate. These models represent geophysical variables on fixed grids and so a comparison among models, with observations, or with other data products must reconcile the differences between variables registered on one set of grid locations to another set. Regridding is a ubiquitous preprocessing step for climate model analysis to interpolate from one gridded field to another. Common grid interpolation methods include kriging, cokriging, bilinear interpolation, inverse distance weighting, and thin plate splines (see McGinnis et al. (2010) for more details). The uncertainty in these statistical and numerical interpolations has been well-documented (Phillips and Marks (1996); Loghmari et al. (2018)). However, to our knowledge this uncertainty is rarely factored into the analysis when a regridded field is considered. In the worst case regridded fields are distributed without the metadatas acknowledging the transformation from their native grid. Moreover, when regridded variables are used for a subsequent analysis, biases can be introduced into statistical estimates.
This work is motivated by the practical issue of inferring the distribution of solar radiation across space and over the seasonal cycle from simulations provided by RCMs. The overall goal is to create a solar radiation data product at a high spatial and temporal resolution that is suitable for siting new solar power generation facilities, such as photo-voltaic plants. Since these facilities may have a lifetime of 30 or more years, it is important to factor in regional changes in climate in site planning. The projections from a multi-model ensemble of RCM projections can suggest the potential impacts of a changing climate on power generation. However, we anticipate biases in the regional model simulations as well as the need to combine several models in an optimal way. The National Solar Radiation Database (NSRDB) is a high resolution, gridded data product that can be used as a standard for calibration under current climate and is a benchmark training and testing sample. The initial step then is to build a statistical model that relates the regional climate model data, forced by reanalysis, to a "gold standard" solar radiation data product (NSRDB).
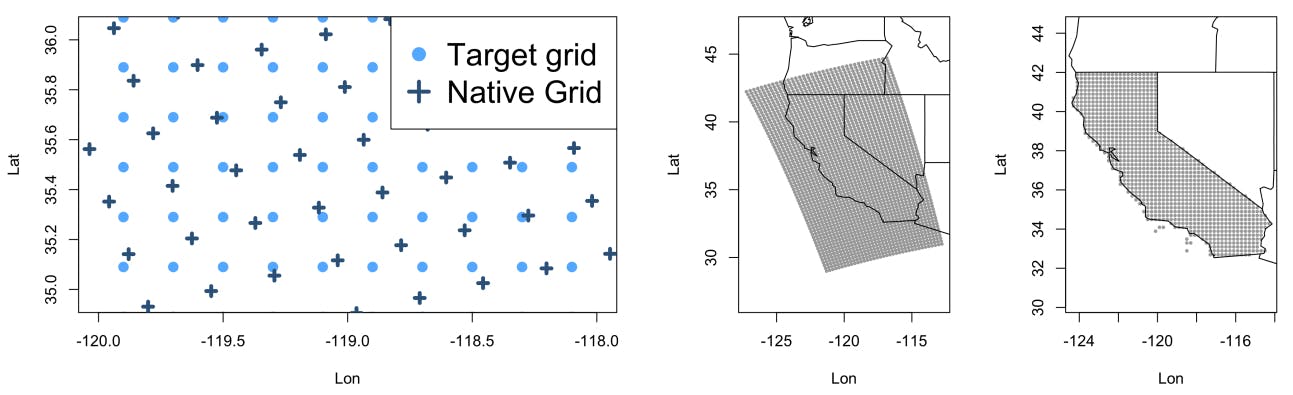
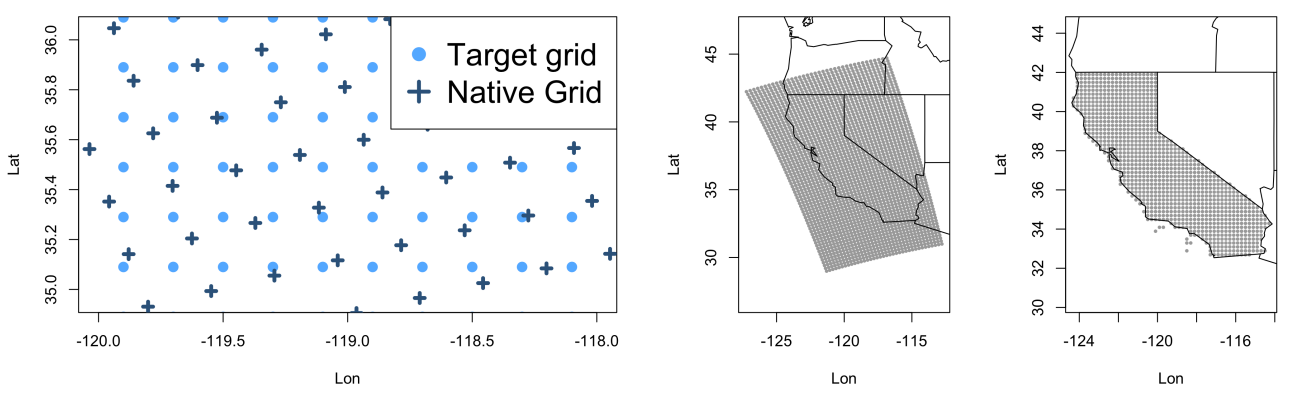
Our focus is on a linear model with NSRDB daily averages as the dependent variable and three RCMs as the independent variables for prediction. The challenge is that the native grid for these models is not the same as the NSRDB, leading to the need for regridding. For illustration, consider Figure 1 showing grid projections from two different models. The differing projections result in an irregular pattern where some target grid locations are close to a native grid point while others fall in between grid locations. It is reasonable to assume that target grid locations that are close to native ones are more accurately interpolated than those further away and this varying uncertainty should be considered in the regridded version.
We contrast the approach of just using the regridded RCM fields as the regression predictors with an empirical Bayesian model that explicitly incorporates the mismatch between the RCM grids and the NSRDB grid. The Bayesian approach takes advantage of recent tools in spatial statistics for conditional simulation of Gaussian processes and combines this with classical Bayesian formulas for linear regression (Cressie and Wikle (2011)). This strategy provides a simple framework to avoid the biases in an analysis based on a regridded estimate. Moreover this method can be extended to more sophicated prediction beyond a linear relationship. Our empirical Bayesian method uses the same spatial prediction model that would be used in standard regridding but adds a step to generate conditional samples of the spatial fields. These realizations then become the conditioned covariate in a Bayesian linear model and with a closed form expression for sampling the posterior of the regression parameters. The Bayesian approach is useful for determining unbiased estimates of the regression parameters. However, if the goal is simply prediction based on the linear model, we also show the standard regridding regression is appropriate for prediction, especially when prediction uncertainty is calibrated with a holdout sample. Therefore, how this problem is tackled depends partly on the end goals of the analysis.
We illustrate these ideas with an application to solar radiation prediction and these results are important in their own right. The analysis suggests the limits of predictability of solar radiation based on regional climate model simulations and also points to how the models may be biased relative to the NSRDB data set.
The uncertainty in the regridding process for solar radiation has not been given much attention as it relates to climate simulations, but there are many studies of this issue for precipitation or temperature (Chandler et al. (2022); Rajulapati et al. (2021)). McGinnis et al. (2010) considered regridding error for RCMs in four regridding methods - nearest neighbors, bilinear interpolation, inverse distance weights, and thin plate splines for temperature and precipitation RCM data. The study found that thin plate splines performed the best of the four considered in terms of regridding but that the chosen interpolation method has a larger effect when considering local results as opposed to large-scale phenomenon across multiple models. Additionally, spurious extrapolation results need to be considered, particularly when considering extreme events, which temperature and precipitation analyses often do. The need for regridding was bypassed in Harris et al. (2022) which proposes Neural-Network Gaussian Process Regression (NNGPR) for predicting temperature and precipitation reanalysis fields from ECMWF Reanalysis v5. The proposed method simultaneously downscales the same variables to RCM spatial levels using NA-CORDEX RCM data for validation. The method defines the downscaling pixel by pixel for the output grid by averaging the input climate model fields and defining a Gaussian process between the climate model fields and prediction point in the reanalysis field. Preliminary results from this study show marginal improvements over existing methods, including linear models, for combining climate models and poor uncertainty quantification skill, which is a direct focus of this study. Additionally, there are minimal metrics for uncertainty quantification of the method. While our method does not simultaneously downscale solar radiation data, this will be addressed in future work and the methods proposed in Harris et al. (2022) could be used for a comparative analysis.
Effects of regridding on precipitation statistics has also been widely studied (Accadia et al. (2003); Berndt and Haberlandt (2018); Ensor and Robeson (2008); Diaconescu et al. (2015); Rauscher et al. (2010)). In particular, effects from regridding were found to have the largest impact at higher quantiles (Rajulapati et al. (2021)). The same study also found that the difference in precipitation statistics between the original and regridded data decreased with higher grid resolution, and vice-versa for lower resolution. This is also true at fine temporal scales (i.e. daily, sub-daily).
Our understanding is that there is a gap in the literature in analyzing the downstream effects on modelling after regridding, and for solar radiation data in particular. Note that this focus is related to the classic errors in variables models (Whittemore (1989)), where covariates are unknown or contain problematic data. Predictions based on the covariates containing error are reliable provided data with the errors is consistently used. However, inferring scientific relationships between the predictand and predictors is not reliable. Thus the focus in this study is whether final conclusions based on downstream modeling and evaluation of an RCM contribution to prediction skill will change when regridding uncertainty is taken into account. As noted above, this study includes an analysis of possible effects using a Bayesian regression approach in order to quantify the uncertainty due to regridding. In particular, we develop a Bayesian hierarchical model (BHM) as a complete description of the analysis uncertainties and then explain how simpler approaches result from approximations to this BHM (Cressie and Wikle (2011)). Although we do not showcase a complete Bayesian analysis, we believe our approximate version is informative and is more easily implemented than the full Bayesian posterior computations.
The rest of the article is organized as follows: Section 2 introduces and describes the data utilized in this article, followed by an overview of the BHM in Section 3; Section 4 details the method to analyze the uncertainty of regridding; Section 5 shows results from this analysis; and finally, Section 6 concludes this work and discusses future directions.
This paper is available on arxiv under CC 4.0 license.